Анхны тоо (төгсгөл)
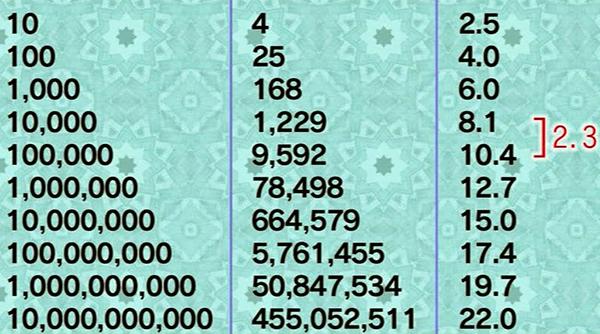
Анхны тоо том болохын хэрээр нэгэн бүтэц тодроод ирлээ. 1 - 1000 хүртэл 168 ширхэг анхны тоо байна гэдэг бол, ойролцоогоор “6 тоо тутмын 1” нь анхны тоо байнаа гэсэн үг.
өмнөх - Анхны тоо (1р хэсэг)
Анхны тоо том болохын хэрээр нэгэн бүтэц тодроод ирлээ. 1 - 1000 хүртэл 168 ширхэг анхны тоо байна гэдэг бол, ойролцоогоор “6 тоо тутмын 1” нь анхны тоо байнаа гэсэн үг.
10,000 хүртэл ойролцоогоор “8 тоо тутмын 1”, 100,000 хүртэл ойролцоогоор “10 тоо тутмын 1” нь анхны тоо.
10 дахин томрохын хэрээр, анхны тоо гарч ирэх магадлал буурч байна.
Бүр нарийн хэлбэл 1,000 хүртэл “6.0-д 1 ширхэг”.
10,000 хүртэл “8.1-д 1 ширхэг”.
100,000 хүртэл “10.4-д 1 ширхэг”.
1,000,000 хүртэл “12.7-д 1 ширхэг”.
Тодорч ирсэн бүтэц гэдэг нь, магадлалын буурах хэмжээ байсан аж.
8.1-с 10.4-ийн хоорондох зөрөө “2.3”.
10.4-с 12.7-ийн хоорондох зөрөө “2.3”.
Профессор Сотой:
-Бага зэргийн хэлбэлзэл байгаа ч, үндсэндээ бол энэ бүтэц цааш үргэлжлээд явна. Өнгөц харахад ямар ч эмх цэгцгүй мэт анхны тоон зүй тогтол ингэж анх тодрон гарч ирсэн юм.
Модыг харалгүй ойг хар. Анхны тоог ширхэгчлэн харахаа больсон Гаусс тэрхүү “тойм зүй тогтлыг” олж анзаарчээ.
-Гаусс анхны тоон ширхэгийн талаарх энэ зүй тогтолыг нээж байхдаа дөнгөж 15 настай балчир хүү байсан гээд бодохоор үнэхээр гайхмаар!.
Гэвч хоёргүй үнэнийг эрэлхийлэх математикчид Гауссын нээсэн “тойм зүй тогтлыг” илүү нарийвчлалтай болгохыг хүсч байлаа.
Түүнд хүчээ сорьсон хүн бол Гауссын шавь Риман юм. Түүний алдарт “Риманы таамаг” гэх уулга алдам нээлт эндээс эхтэй.
Тэр бол математикийн ертөнцийн хамгийн хүнд бодлого. Түүнд нь комплекс анхны тоо болон хуурмаг тоо, аналитик функц, Зетта функц зэрэг хамгийн ярвигтай элементүүд холилдон гарч ирнэ.
Түүнийг Сотой профессор дуутай зүйрлүүлэн, дараах байдлаар хялбарчлан тайлбарлав.
-Риманы хийсэн зүйл бол, “анхны тоонд нуугдах чимээнд” чихээ тавин сонсох явдал байсан юм.
Үүнийг ойлгохын өмнөх суурь мэдлэг болгож, дууны тухай бага зэрэг мэдэх шаардлагатай.
Математикийн суурь нэгжийг анхны тоо юм гэвэл, дууны түүнд харгалзах зүйл нь хөглөгч буюу “камертон” юм, гэж Францын математикч Фурье хэлсэн нь бий.

Камертоноос гарах дуу бол дуунууд дотроо хамгийн цэвэр нь байдаг бөгөөд, түүний дууны долгион нь “зөв синусын долгионыг” зурдаг.
Нөгөөтэйгүүр хийл мэтийн зэмсгээс гарах дууны долгион нь “чичирхийлэн мур илзсан долгион” байдаг. Тэр бол олон тооны цэвэр дуунууд (буюу синусын долгиону уд) давхралдан бүтсэн дуу юм.
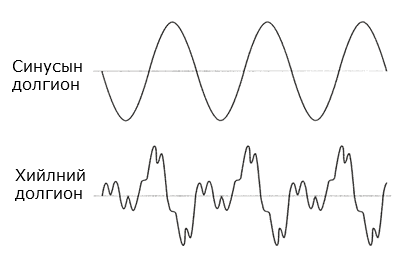
Хийлнээс гарах синусын долгионы давтамж нь хийлний утасны уртаас хамаарна. Тэр нь суурь долгион болж, түүн дээр ахиад “гармоник” гэгдэх хэд хэдэн долгион нэмэгдэн давхцана.
Жишээ нь, компьютерт камертоны цэвэр дуунд нэг нэгээр гармоник долгионыг нэмээд явахад, тэр нь шат шиг болон хэлбэрээ өөрчилж, шинэ гармоник нэмэгдэх бүрт шатны гишгүүр нь олон болоод явдаг.
-Энэ санааг толгойдоо буулгаж чадвал, Риманы хийсэн ажлыг амархан ойлгож чадна. Нэг ёсондоо, анхны тоон шатыг дуу гэж төсөөлөхөд болох юм.
Гауссын анх бүтээсэн “анхны тоон шат” бол зүйрлүүлбээс “камертоны дуу (суурь долгион)” шиг зүйл байв. Түүнд нь Риман Зетта функц, комплекс анхны тоо гэсэн, нэг ёсны гармоникууд нэмж өгсөөр Гауссын графыг илүү нарийвчлалтай болгон янзалсан учиртай.
-Ингээд Риманы нээлтийг толилуулъя. Хэрвээ эзгүй арал руу ганц зүйл авч явж болно гэвэл, би Риманы томъёог л сонгох болов уу.
Гауссын логарифм ашиглан гаргаж ирсэн анхны тоон шатны граф бол, анхны тоон тархалтыг ерөнхийд нь илэрхийлдэг боловч өндөр нарийвчлалтай биш юм. Түүнд нь Риманы гармоник долгионуудыг нэмснээр түүний нарийвчлал өндөрсөөд явна.
Профессор Сотойн тайлбараар бол
-Хийлний дууг бүрдүүлдэг гармоникуудыг нэг бүрчлэн нэмснээр жинхэнэ хийлний аяыг бүтээдгийн адилаар, граф ч бас агшиж сунаж явсаар өндөр нарийвчлалтай “анхны тоон шатанд” ойртох болно.
Дашрамд хэлэхэд хийлний дууг компьютерт дүрслэхэд ч бас дээрхтэй адилхан аргыг хэрэглэдэг. Суурь долгион болох камертоны дуунд хэд хэдэн гармоник давхарлан тоглуулах байдлаар хийлний дуунд ойртуулан тохируулдаг. 100 ширхэг гармоник давхарлахад, Риманы граф дотор ч Гауссын анхны тоон шат дүрслэгдээд ирнэ.
-100 ширхэг хүртэл долгион давхарлахад, жишээ нь “23 ба 29-ын хооронд анхны тоо байхгүй” болох нь тодроод ирнэ. Харин үүнийг бол Гауссын графаас харах боломжгүй.

Риманы олж харсан нь цаашлаад улам гайхмаар зүйл байв. Ойн моддыг анхааралтайгаар ажиглан шинжилтэл нэгэн нууцлаг зүй тогтол ойн гүнээс илэрчээ.
-Жишээлбэл, та нар CD тоглуулагчаар хөгжим сонсохдоо дууны их багыг (буюу өндөр) нь тохируулдаг шүү дээ. Түүнтэй адилаар Риман долгионы давтамж болон өндрийг нь өөр өөр графанд эмхэтгэж үзэж. Тэгтэл гайхалтайгаар, давтамжууд бүгд харилцан өөр боловч, долгионы өндрүүд нь бүгд ижил байх юм гэнэ. Бүх дуунууд яг илбэдүүлсэн юм шиг нэг шулуун дээр эгнэж байх нь тэр.
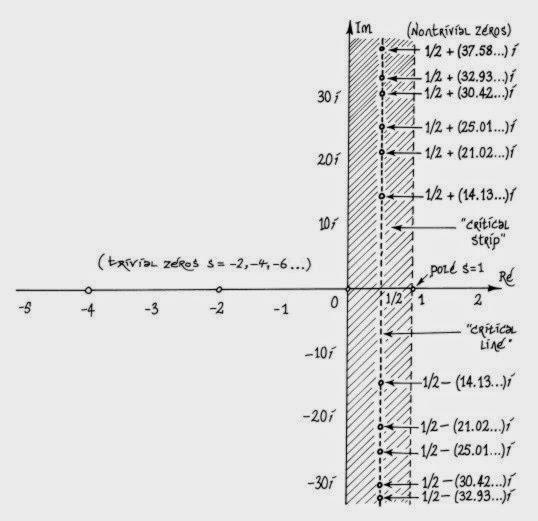
Цэгээр дүрслэхэд энд тэндгүй байлаа гээд гайхах явдалгүй баймаар өндрүүд хачирхалтайгаар төгс зэрэгцэж байв. Энэ бол яавч тохиолдлын гэж бодохын аргагүй. Уг шулуун хожимоо “Риманы онцгой шулуун (critical line)” гэж нэрлэгдэх болно.
-Риман эхлээд 10 ширхэг долгион дээр туршиж үзтэл ийнхүү цэвэрхэн эгнэж байсан тул, тэрээр бүх долгионууд онцгой шулуун дээр байрлана хэмээн таамаглажээ.
Үүнийг алдарт “Риманы таамаг” гэдэг.
-Хэрвээ энэ шулуунаас гадуур дуу байна гэвэл, тэр дуу бусадтайгаа харьцуулахад тэс хөндлөн өндөр дуу болж сонсогдоно. Оркестр сонсож байтал гэв гэнэт баргил бүрээ дундуур орж ирээд хамаг хэмнэл баллаад хаяхтай л адил юм болно.
Үнэхээр анхны тоо хэмээх оркестр бүгд ижилхэн өндөртэй дуугаар хөгжимддөг юм болов уу?
Хэрэв тийм бол Риманы таамаг үнэн гэсэн үг болно. Нөгөөтэйгүүр, байж боломгүй хөндлөн баргил бүрээ байдаг гэвэл, Риманы таамаг нурна. Гэвч одоогийн байдлаар тийм бүрээ олсон хүн нэгээхэн ч алга. Өөрөөр хэлбэл, Риманы таамаг одоо болтол батлагдаагүй л байгаа юм.
Бүрхан шоо шидээд байна уу гэлтэй санамсаргүй гарч ирэх анхны тоонууд.
Гэвч Риманы таамгаар бол, тэр шоо тодорхой нэг хүрээнээс хэрхэвч гарах явдал үгүй. Санамсаргүйн дунд нэг төрлийн жигдхэн зүй тогтол үйлчилж байна хэмээн Риман таамагласан нь тэр юм.
Үүнийг Сотой профессор өрөөн доторх хүчилтөрөгчтэй зүйрлүүлнэ.
-Агаар доторх молекул нэг бүрийг хаана байгааг нарийвчлан хэлэх ямар ч боломжгүй. Гэвч, өрөөний хаа нэг буланд очтол тэнд гэнэт ямар ч хүчилтөрөгч байхгүй болж бүтэх явдал хэзээ ч гардаггүй шүү дээ. Санамсаргүй ч гэлээ молекулууд агаар дотор жигдхэн тархсан байдаг.
Агаар доторх алив нэг хүчилтөрөгч хаана байх үнэндээ тийм ч чухал биш. Харин хүчилтөрөгч хаа сайгүй тархсан байгаа нь чухал юм.
-Математикчдын хувьд ч бас анхны тооны талаар мэдэх шаардлагатай байсан нь үнэндээ ийм л зүйл байсан. Бүгдийг мэдэх шаардлагагүй. Эсрэгээрээ тархалтыг нь мэдэж байхад л хангалттай юм.
Анхны тоон их ой байгаа нь нүдний өмнө илхэн боловч, түүний мод нэг бүр нь хаана хаана ургаж буй нь одоо ч нууц хэвээр.
Риманы таамгийг (зөв эсвэл буруу эсэхийг нь) баталж чадсан математикчийг Америкийн Клейн математикийн судалгааны хүрээлэнгээс 1 сая доллараар байлаад байгаа билээ.
Эсрэгээрээ анхны тооны тэрхүү зүй тогтолгүй байдлыг хүн төрөлхитөн хэдийнэ ашиглаад эхэлжээ.
Интернет дэхь аюулгүй байдлыг баталгаажуулах “нууцлал” нь тэр юм.
Жишээ нь, 9999911 гэдэг тоо байг. Энэ тоо 2 анхны тоон үржвэрээс бүтдэг. Нууцлалыг тайлах түлхүүр нь, хэлбээс тэр хоёр тоо юм.
-Та кредит картаараа интернэтээр худалдаа хийх гэж байна гэж бодъё. Мэдээж картныхаа дугаарыг нууцлах шаардлагатай. Чингүүт дэлгүүрээс танд дээрх шиг тоо илгээнэ. Бодитоор бол хамаагүй том тоо ашигладаг л даа. Ингээд уг тоо болон картны дугаарыг ашигласан нууц код хийгдэж, дэлгүүртэй та аюулгүйгээр наймаа хийж чадах болно.
Хэрвээ тэр нууц кодыг хялбархан анхны тоонд задалдаг томьёо олдчих юм бол, нууцалсан тоо нь бултайтал илэрч орхино. Харин анхны тоонд одоохондоо тийм томьёо олдоогүй л байна.
Тиймээс анхны тоог ашигласан нууцлалыг тайлъя гэвэл тоймгүй их хугацаа хөдөлмөр орох болно. Чухам энэ л интэрнет дэхь нууцлал аюулгүй болохын баталгаа болж байдаг юм.
Сотой профессор:
-Ямар ч байсан өнөөдрийн интэрнет дэхь нууцлал бол, анхны тоог олдог томьёо олдоогүй гэдэг нөхцөл дээр суурилж байдаг.
Дашрамд хэлэхэд, 9999911 гэдэг тоо бол “307” ба “32573” гэх хоёр анхны тооны үржвэр. Ийм дайны бяцхан тооны хувьд бол, үүнийг бодоод өгөх програмууд интэрнетээр нэг бэлчиж байгаа.
Математикийн ертөнцийн хамгийн том сорилт “Анхны тоо”.
-Химийн бодисыг атом цөм болгон задалж чадах атал, тоог анхны тоонд задлах хялбар арга одоо болтол олдоогүй л байна.
Хэдий тийм ч, хэзээ нэгэн цагт Риманы таамаг хүртэл батлагдах цаг ирж л таарах болов уу.
-Гэхдээ тэр үр дүнгээс илүүтэй, тэр хүртлэх замнал нь өөрөө бид бүхний үлэмж баялаг байх биз ээ.
хэмээн Сотой профессор итгэл дүүрэн хэлнэ.
-Миний хувьд математик амьд мэдлэгийн салбар гэж санагддаг нь, энэ мэт асуудлуудын ач юм. Риманы таамаг, анхны тоонд хүчээ сорьсоноор л сая би математикийн тэр часхийсэн аагийг мэдэрч чаддаг юм даа.
...Жоохон яриа халуурахад, саяхан би нүүгээд, утасныхаа дугаарыг солих боллоо л доо. Тэгээд оператор компанид шинэ утасны дугаар авъя гэж хүсэлт гаргасан юм. Тэгсэн хариуцагч хүүхэн надад нэг дугаар оноож өгөв өө. Хартал тэр нь анхны тоо биш байна. Тэгэхээр нь би цээжлэхэд хэцүү юм энэ тэр гэж худлаа шалтаглаж байгаад өөр дугаар авахаар боллоо.
Лондоны утасны дугаар 8 оронтой. Тоогоор хэлбэл 10,000,000 гэсэн үг. Шинэ дугаар анхны тоо байх магадлал Гауссын анхны тоон шатаар бол “15-д нэг”. Өөрөөр хэлбэл 15 удаа дугаараа солиулахад анхны тоонд буух магадлал өндөр байсан юм.
Тэгтэл дараагийн дугаар ч бас анхны тоо биш байна шүү.
Ингээд хэд дахиад дугаараа солиултал, аргагүй нөгөө хүүхэн чинь уурлаж байна. Би ч уучлал гуйгаад, яг дараагийн дугаарыг үг дуугүй авах болноо гэдгээ хэллээ.
Харин тэр дугаар нь тэгш тоо байсан даа. Даанч гомдмоор...
- Цэгцэрсэн шат
Анхны тоо том болохын хэрээр нэгэн бүтэц тодроод ирлээ. 1 - 1000 хүртэл 168 ширхэг анхны тоо байна гэдэг бол, ойролцоогоор “6 тоо тутмын 1” нь анхны тоо байнаа гэсэн үг.
10,000 хүртэл ойролцоогоор “8 тоо тутмын 1”, 100,000 хүртэл ойролцоогоор “10 тоо тутмын 1” нь анхны тоо.
10 дахин томрохын хэрээр, анхны тоо гарч ирэх магадлал буурч байна.
Бүр нарийн хэлбэл 1,000 хүртэл “6.0-д 1 ширхэг”.
10,000 хүртэл “8.1-д 1 ширхэг”.
100,000 хүртэл “10.4-д 1 ширхэг”.
1,000,000 хүртэл “12.7-д 1 ширхэг”.
Тодорч ирсэн бүтэц гэдэг нь, магадлалын буурах хэмжээ байсан аж.
8.1-с 10.4-ийн хоорондох зөрөө “2.3”.
10.4-с 12.7-ийн хоорондох зөрөө “2.3”.

Профессор Сотой:
-Бага зэргийн хэлбэлзэл байгаа ч, үндсэндээ бол энэ бүтэц цааш үргэлжлээд явна. Өнгөц харахад ямар ч эмх цэгцгүй мэт анхны тоон зүй тогтол ингэж анх тодрон гарч ирсэн юм.
Модыг харалгүй ойг хар. Анхны тоог ширхэгчлэн харахаа больсон Гаусс тэрхүү “тойм зүй тогтлыг” олж анзаарчээ.
-Гаусс анхны тоон ширхэгийн талаарх энэ зүй тогтолыг нээж байхдаа дөнгөж 15 настай балчир хүү байсан гээд бодохоор үнэхээр гайхмаар!.
- Риман
Гэвч хоёргүй үнэнийг эрэлхийлэх математикчид Гауссын нээсэн “тойм зүй тогтлыг” илүү нарийвчлалтай болгохыг хүсч байлаа.
Түүнд хүчээ сорьсон хүн бол Гауссын шавь Риман юм. Түүний алдарт “Риманы таамаг” гэх уулга алдам нээлт эндээс эхтэй.
Тэр бол математикийн ертөнцийн хамгийн хүнд бодлого. Түүнд нь комплекс анхны тоо болон хуурмаг тоо, аналитик функц, Зетта функц зэрэг хамгийн ярвигтай элементүүд холилдон гарч ирнэ.
Түүнийг Сотой профессор дуутай зүйрлүүлэн, дараах байдлаар хялбарчлан тайлбарлав.
-Риманы хийсэн зүйл бол, “анхны тоонд нуугдах чимээнд” чихээ тавин сонсох явдал байсан юм.
Үүнийг ойлгохын өмнөх суурь мэдлэг болгож, дууны тухай бага зэрэг мэдэх шаардлагатай.
Математикийн суурь нэгжийг анхны тоо юм гэвэл, дууны түүнд харгалзах зүйл нь хөглөгч буюу “камертон” юм, гэж Францын математикч Фурье хэлсэн нь бий.

Камертоноос гарах дуу бол дуунууд дотроо хамгийн цэвэр нь байдаг бөгөөд, түүний дууны долгион нь “зөв синусын долгионыг” зурдаг.
Нөгөөтэйгүүр хийл мэтийн зэмсгээс гарах дууны долгион нь “чичирхийлэн мур илзсан долгион” байдаг. Тэр бол олон тооны цэвэр дуунууд (буюу синусын долгиону уд) давхралдан бүтсэн дуу юм.

Хийлнээс гарах синусын долгионы давтамж нь хийлний утасны уртаас хамаарна. Тэр нь суурь долгион болж, түүн дээр ахиад “гармоник” гэгдэх хэд хэдэн долгион нэмэгдэн давхцана.
Жишээ нь, компьютерт камертоны цэвэр дуунд нэг нэгээр гармоник долгионыг нэмээд явахад, тэр нь шат шиг болон хэлбэрээ өөрчилж, шинэ гармоник нэмэгдэх бүрт шатны гишгүүр нь олон болоод явдаг.
-Энэ санааг толгойдоо буулгаж чадвал, Риманы хийсэн ажлыг амархан ойлгож чадна. Нэг ёсондоо, анхны тоон шатыг дуу гэж төсөөлөхөд болох юм.
Гауссын анх бүтээсэн “анхны тоон шат” бол зүйрлүүлбээс “камертоны дуу (суурь долгион)” шиг зүйл байв. Түүнд нь Риман Зетта функц, комплекс анхны тоо гэсэн, нэг ёсны гармоникууд нэмж өгсөөр Гауссын графыг илүү нарийвчлалтай болгон янзалсан учиртай.
- Гармоник долгион
-Ингээд Риманы нээлтийг толилуулъя. Хэрвээ эзгүй арал руу ганц зүйл авч явж болно гэвэл, би Риманы томъёог л сонгох болов уу.
Гауссын логарифм ашиглан гаргаж ирсэн анхны тоон шатны граф бол, анхны тоон тархалтыг ерөнхийд нь илэрхийлдэг боловч өндөр нарийвчлалтай биш юм. Түүнд нь Риманы гармоник долгионуудыг нэмснээр түүний нарийвчлал өндөрсөөд явна.
Профессор Сотойн тайлбараар бол
-Хийлний дууг бүрдүүлдэг гармоникуудыг нэг бүрчлэн нэмснээр жинхэнэ хийлний аяыг бүтээдгийн адилаар, граф ч бас агшиж сунаж явсаар өндөр нарийвчлалтай “анхны тоон шатанд” ойртох болно.
Дашрамд хэлэхэд хийлний дууг компьютерт дүрслэхэд ч бас дээрхтэй адилхан аргыг хэрэглэдэг. Суурь долгион болох камертоны дуунд хэд хэдэн гармоник давхарлан тоглуулах байдлаар хийлний дуунд ойртуулан тохируулдаг. 100 ширхэг гармоник давхарлахад, Риманы граф дотор ч Гауссын анхны тоон шат дүрслэгдээд ирнэ.
-100 ширхэг хүртэл долгион давхарлахад, жишээ нь “23 ба 29-ын хооронд анхны тоо байхгүй” болох нь тодроод ирнэ. Харин үүнийг бол Гауссын графаас харах боломжгүй.

- Дууны өндөр
Риманы олж харсан нь цаашлаад улам гайхмаар зүйл байв. Ойн моддыг анхааралтайгаар ажиглан шинжилтэл нэгэн нууцлаг зүй тогтол ойн гүнээс илэрчээ.
-Жишээлбэл, та нар CD тоглуулагчаар хөгжим сонсохдоо дууны их багыг (буюу өндөр) нь тохируулдаг шүү дээ. Түүнтэй адилаар Риман долгионы давтамж болон өндрийг нь өөр өөр графанд эмхэтгэж үзэж. Тэгтэл гайхалтайгаар, давтамжууд бүгд харилцан өөр боловч, долгионы өндрүүд нь бүгд ижил байх юм гэнэ. Бүх дуунууд яг илбэдүүлсэн юм шиг нэг шулуун дээр эгнэж байх нь тэр.

Цэгээр дүрслэхэд энд тэндгүй байлаа гээд гайхах явдалгүй баймаар өндрүүд хачирхалтайгаар төгс зэрэгцэж байв. Энэ бол яавч тохиолдлын гэж бодохын аргагүй. Уг шулуун хожимоо “Риманы онцгой шулуун (critical line)” гэж нэрлэгдэх болно.
-Риман эхлээд 10 ширхэг долгион дээр туршиж үзтэл ийнхүү цэвэрхэн эгнэж байсан тул, тэрээр бүх долгионууд онцгой шулуун дээр байрлана хэмээн таамаглажээ.
Үүнийг алдарт “Риманы таамаг” гэдэг.
-Хэрвээ энэ шулуунаас гадуур дуу байна гэвэл, тэр дуу бусадтайгаа харьцуулахад тэс хөндлөн өндөр дуу болж сонсогдоно. Оркестр сонсож байтал гэв гэнэт баргил бүрээ дундуур орж ирээд хамаг хэмнэл баллаад хаяхтай л адил юм болно.
Үнэхээр анхны тоо хэмээх оркестр бүгд ижилхэн өндөртэй дуугаар хөгжимддөг юм болов уу?
Хэрэв тийм бол Риманы таамаг үнэн гэсэн үг болно. Нөгөөтэйгүүр, байж боломгүй хөндлөн баргил бүрээ байдаг гэвэл, Риманы таамаг нурна. Гэвч одоогийн байдлаар тийм бүрээ олсон хүн нэгээхэн ч алга. Өөрөөр хэлбэл, Риманы таамаг одоо болтол батлагдаагүй л байгаа юм.
Бүрхан шоо шидээд байна уу гэлтэй санамсаргүй гарч ирэх анхны тоонууд.
Гэвч Риманы таамгаар бол, тэр шоо тодорхой нэг хүрээнээс хэрхэвч гарах явдал үгүй. Санамсаргүйн дунд нэг төрлийн жигдхэн зүй тогтол үйлчилж байна хэмээн Риман таамагласан нь тэр юм.
Үүнийг Сотой профессор өрөөн доторх хүчилтөрөгчтэй зүйрлүүлнэ.
-Агаар доторх молекул нэг бүрийг хаана байгааг нарийвчлан хэлэх ямар ч боломжгүй. Гэвч, өрөөний хаа нэг буланд очтол тэнд гэнэт ямар ч хүчилтөрөгч байхгүй болж бүтэх явдал хэзээ ч гардаггүй шүү дээ. Санамсаргүй ч гэлээ молекулууд агаар дотор жигдхэн тархсан байдаг.
Агаар доторх алив нэг хүчилтөрөгч хаана байх үнэндээ тийм ч чухал биш. Харин хүчилтөрөгч хаа сайгүй тархсан байгаа нь чухал юм.
-Математикчдын хувьд ч бас анхны тооны талаар мэдэх шаардлагатай байсан нь үнэндээ ийм л зүйл байсан. Бүгдийг мэдэх шаардлагагүй. Эсрэгээрээ тархалтыг нь мэдэж байхад л хангалттай юм.
Анхны тоон их ой байгаа нь нүдний өмнө илхэн боловч, түүний мод нэг бүр нь хаана хаана ургаж буй нь одоо ч нууц хэвээр.
Риманы таамгийг (зөв эсвэл буруу эсэхийг нь) баталж чадсан математикчийг Америкийн Клейн математикийн судалгааны хүрээлэнгээс 1 сая доллараар байлаад байгаа билээ.
- Нууцлал
Эсрэгээрээ анхны тооны тэрхүү зүй тогтолгүй байдлыг хүн төрөлхитөн хэдийнэ ашиглаад эхэлжээ.
Интернет дэхь аюулгүй байдлыг баталгаажуулах “нууцлал” нь тэр юм.
Жишээ нь, 9999911 гэдэг тоо байг. Энэ тоо 2 анхны тоон үржвэрээс бүтдэг. Нууцлалыг тайлах түлхүүр нь, хэлбээс тэр хоёр тоо юм.
-Та кредит картаараа интернэтээр худалдаа хийх гэж байна гэж бодъё. Мэдээж картныхаа дугаарыг нууцлах шаардлагатай. Чингүүт дэлгүүрээс танд дээрх шиг тоо илгээнэ. Бодитоор бол хамаагүй том тоо ашигладаг л даа. Ингээд уг тоо болон картны дугаарыг ашигласан нууц код хийгдэж, дэлгүүртэй та аюулгүйгээр наймаа хийж чадах болно.
Хэрвээ тэр нууц кодыг хялбархан анхны тоонд задалдаг томьёо олдчих юм бол, нууцалсан тоо нь бултайтал илэрч орхино. Харин анхны тоонд одоохондоо тийм томьёо олдоогүй л байна.
Тиймээс анхны тоог ашигласан нууцлалыг тайлъя гэвэл тоймгүй их хугацаа хөдөлмөр орох болно. Чухам энэ л интэрнет дэхь нууцлал аюулгүй болохын баталгаа болж байдаг юм.
Сотой профессор:
-Ямар ч байсан өнөөдрийн интэрнет дэхь нууцлал бол, анхны тоог олдог томьёо олдоогүй гэдэг нөхцөл дээр суурилж байдаг.
Дашрамд хэлэхэд, 9999911 гэдэг тоо бол “307” ба “32573” гэх хоёр анхны тооны үржвэр. Ийм дайны бяцхан тооны хувьд бол, үүнийг бодоод өгөх програмууд интэрнетээр нэг бэлчиж байгаа.
- Амьд мэдлэгийн салбар
Математикийн ертөнцийн хамгийн том сорилт “Анхны тоо”.
-Химийн бодисыг атом цөм болгон задалж чадах атал, тоог анхны тоонд задлах хялбар арга одоо болтол олдоогүй л байна.
Хэдий тийм ч, хэзээ нэгэн цагт Риманы таамаг хүртэл батлагдах цаг ирж л таарах болов уу.
-Гэхдээ тэр үр дүнгээс илүүтэй, тэр хүртлэх замнал нь өөрөө бид бүхний үлэмж баялаг байх биз ээ.
хэмээн Сотой профессор итгэл дүүрэн хэлнэ.
-Миний хувьд математик амьд мэдлэгийн салбар гэж санагддаг нь, энэ мэт асуудлуудын ач юм. Риманы таамаг, анхны тоонд хүчээ сорьсоноор л сая би математикийн тэр часхийсэн аагийг мэдэрч чаддаг юм даа.
...Жоохон яриа халуурахад, саяхан би нүүгээд, утасныхаа дугаарыг солих боллоо л доо. Тэгээд оператор компанид шинэ утасны дугаар авъя гэж хүсэлт гаргасан юм. Тэгсэн хариуцагч хүүхэн надад нэг дугаар оноож өгөв өө. Хартал тэр нь анхны тоо биш байна. Тэгэхээр нь би цээжлэхэд хэцүү юм энэ тэр гэж худлаа шалтаглаж байгаад өөр дугаар авахаар боллоо.
Лондоны утасны дугаар 8 оронтой. Тоогоор хэлбэл 10,000,000 гэсэн үг. Шинэ дугаар анхны тоо байх магадлал Гауссын анхны тоон шатаар бол “15-д нэг”. Өөрөөр хэлбэл 15 удаа дугаараа солиулахад анхны тоонд буух магадлал өндөр байсан юм.
Тэгтэл дараагийн дугаар ч бас анхны тоо биш байна шүү.
Ингээд хэд дахиад дугаараа солиултал, аргагүй нөгөө хүүхэн чинь уурлаж байна. Би ч уучлал гуйгаад, яг дараагийн дугаарыг үг дуугүй авах болноо гэдгээ хэллээ.
Харин тэр дугаар нь тэгш тоо байсан даа. Даанч гомдмоор...






Сод
Талархал
Сонирхолтой