• Түрхэн зуурын цайны цаг

Энэ удаад математикийн олон гишүүнт тэгшитгэлийн ерөнхий томъёоны талаарх нэгэн түүхийг ярьж өгье. Юуны өмнө олон гишүүнт тэгшитгэл гэж юу билээ? Түүнийг математикт доорх байдлаар илэрхийлдэг.

ax+b=0
(1 зэргийн олон гишүүнт тэгшитгэл)
ax²+bx+c=0
(2 зэргийн олон гишүүнт тэгшитгэл)
ax³+bx²+cx+d=0
(3 зэргийн олон гишүүнт тэгшитгэл)
ax⁴+bx³+cx²+dx+e=0
(4 зэргийн олон гишүүнт тэгшитгэл)

(a,b,c,d,e нь дурын бодит тоо. Гэхдээ a≠0)

Нэг ёсондоо “3 зэргийн олон гишүүнт” гэвэл x³-р эхэлсэн тэгшитгэл гээд ойлгочиход бараг л болно. 4 зэргийн гэвэл мэдээж х⁴-р эхэлнэ гэсэн үг.

Онцлог нь, олон гишүүнт тэгшитгэл нь 4 дээр очоод дуусчихгүй, 5 зэргийн олон гишүүнт (x⁵-р эхэлсэн), 6 зэргийн олон гишүүнт (x⁶-р эхэлсэн), цаашлаад дурын n-ын хувьд n зэргийн олон гишүүнт гээд төгсгөлгүй зохиох ч боломжтой.

За тэгэхээр, иймэрхүү олон гишүүнт тэгшитгэлүүдэд х-ын утгыг олох ерөнхий томъёо гээч юм оршин байдаг. Жишээлбэл 2 зэргийн олон гишүүнт тэгшитгэлийн (квадрат тэгшитгэл) томъёо нь нэг иймэрхүү байна.


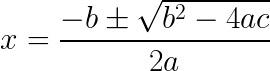
Дээрх томъёог 10 жилд заадаг тул, магадгүй олон хүнд танил санагдаж мэдэх юм. Иймэрхүү томъёоны юу нь сонирхолтой вэ гэхээр, a, b, c-ын утгыг яаж ч өөрчлөөд, ямар ч хэлбэрийн тэгшитгэл зохиолоо гэсэн, ганцхан томъёонд орлуулах төдийд л газар дээр нь хариуг гаргаад тавьчихдагт байгаа юм.

Жишээ нь та төсөөлөөд үз дээ!. Та дээрхи томъёог огт мэдэхгүй байна гэж бодоод “x²+5х+11=0” тэгшитгэлийг хангах х-ын утгыг олоод аль гэж тулгагдвал яах байсан болоо? Томъёог нь мэддэг бол хэнд ч хялбархан атал, мэдэхгүй бол ёстой яахаа мэдэхгүй, бодоод бодоод бодын шир 4 гэгч л болно биз. Ямар ч байсан л, хариуг нь олох гэж эргүүлж тойруулж туршсаар багагүй цаг зарцуулах нь лавтай. Тиймээс ямар нэг тэгшитгэл бодох үед, түүний ерөнхий томъёог мэддэг байх мэдэхгүй байхын хооронд ийм том ялгаа үүснэ ээ л гэсэн үг.

Өнөө үед ч яахав, ямар ч тэгшитгэлийн хариу олдог томъёог нэтээс хайхад л ярайтал гараад ирнэ. Харин дээр үед байсан бол иймэрхүү томъёонууд нь “тооны илбэ” гэгдэн олон нийтэд түгээгдэх явдал байгаагүй юм. Тэр бүү хэл ийм томъёог олж нээсэн математикч нь найз математикчиддаа ч хэлье гэдэггүй байв.

Яагаад математикийн томъёо нь “тооны илбэ” гэгддэг байсан бээ гэхээр, тэр нь 16-р зууны үеийн математикчидын онцгой нөхцөл байдлаас улбаатай байжээ.

Тухайн үеийн математикчид ажлынхаа хажуугаад “тоо бүртгэгч” хэмээх халтуурны ажил давхар хийж, худалдаачдад мэргэжлийн тооцоолон бодогчийн алба хаан чамгүй орлого олдог байж. Тиймээс олны дунд “сайн тоочин” гэсэн нэр хүндээ хадгалж явах нь үхэл сэхлийн дайтай чухал асуудал байсан хэрэг. Ингээд тухайн үеийн математикийн ертөнцөд худалдаачдад зориулсан үзүүлэн тоглолт хийх далд агуулгатай хурдан бодолтын нээлттэй тэмцээнүүд өргөн дэлгэр зохиогддог байв. Дашрамд хэлэхэд тиймэрхүү тэмцээнд бай шагнал ч дагалдах тул, түрүүлсэн хүн нь алдар нэрээс гадна эд баялгийг ч давхар олдог байжээ.

Тэдгээр математикчдын хувьд томъёо гэдэг бол эгшин зуур бодлого бодон өрсөлдөгчөө дарж авах нууц шившлэг л гэсэн үг. Нээрээ ч, нэг бодлого гарч иртэл тэрийг нь боддог томъёог ганцхан би мэдээд, бусад нь мэдэхгүй байвал шууд л цэвэр ялснаас өөрцгүй шүү дээ.

Ийм цаг үеийн дэвсгэр нөлөөлснөөр, математикчид өөрсдийн давуу талыг хадгалахын тулд шинэ томъёо олж нээсэн ч түүнээ нууцлан, бусдад хэрхэвч үзүүлдэггүй байв.

Дашрамд хэлэхэд, тэрхүү нээлттэй тэмцээнүүдийн бодлогод 3 зэргийн олон гишүүнт тэгшитгэл тавигдах явдал элбэг байжээ. 2 зэргийн олон гишүүнт тэгшитгэлийн томъёо математикчдын дунд нэгэнт бүрэн танигдсан боловч, 3 зэргийн олон гишүүнтийн томъёо хараахан олдоогүй байж. Тиймээс 3 зэргийн олон гишүүнт тэгшитгэл тун ч амттай бодлогод тооцогдон тавигдах нь түгээмэл байж.

Тиймээс эсрэгээр нь хэлбэл, 3 зэргийн олон гишүүнтийн томъёог хэрэв олж чадах юм бол тэмцээнүүдэд дараалан түрүүлж, алдар нэр эд баялагийг ч давхар хамна гэсэн үг. Ингээд математикчид 3 зэргийн олон гишүүнтийн томъёог олохоор үхэн хатан зүтгэж гарчээ.

Хариу олдог ерөнхий томъёог нээж математикийн оргилд гарах нь чухам хэн байх бол?

Олон гишүүнтийн ерөнхий томъёог тойрсон математикчдын ширүүн тулаан ийнхүү эхлэв ээ.

• Зальт Кардано

16-р зууны үед математикчдын дунд 3 зэргийн олон гишүүнт тэгшитгэл бодох нээлттэй тэмцээн өргөн дэлгэр болдог байв. Тухайн үед нээлттэй тэмцээний аварга нь Фиор (Fior) гэгч хүн байжээ. Фиор багшаасаа 3 зэрэгт олон гишүүнт тэгшитгэлийн тооны илбийг өвлөн авч, түүгээрээ ялалтын буухиагаа залгуулдаг байв. Гэхдээ тэр томъёо нь төгс бус, хязгаарлагдмал хэлбэрийн тэгшитгэлд л хүчинтэй эд байсан гэдэг.

Тэгтэл мөн цаг үеэр Тарталья (Tartaglia) хэмээх математикч Фиорыг нээлттэй тэмцээнд зарлан дуудав. Тарталья бол хичээнгүйгээрээ алдартай өндөр нэрт математикч бөгөөд өөрийн хүчээр Фиорын томъёог ч даван гарах, ямар ч 3 зэргийн олон гишүүнтийг бодож чадах төгс томъёог зохион бүтээгээд байж.

Тэмцээн мэдээж Тартальягийн илт давуугаар төгсөж, тэрээр нээлттэй тэмцээний шинэ аварга болон тодорлоо. Амтай болгон 3 зэргийн олон гишүүнтийн томъёог олсон математикчийг шагшин буцална. Олон ч хүн түүнд бараалхан “Хичээнгүйлэн гуйя. Тэр томъёогоо заагаад өгөөч” хэмээн шавалдсан нь тодорхой. Кардано (Cardano) ч бас нэгэн адилаар Тарталья тийш гүйлдсэн хүмүүсийн нэг байлаа. Кардано яаж ийгээд ч болов томъёог заалгаад авчих санаатай Тартальяг уйгагүй шалан зууралдаж гэнэ. Мэдээж хэрэг Тарталья түүнд татгалзсан боловч, Кардано цөхрөлгүй чаргуулдан зүүгдсээр. Сүрдүүлж ч үзэв, наймаалцаж ч үзэв, хэрэглэж болох бүхий л аргаа ашиглан тооны илбийг нь авахаар улайран санаархаж гарчээ.

Дашрамд хэлэхэд, Кардано бол философич, эмч, одон зурхайч, магадлалын онолд тулгуурласан мөрийтэй тоглоомын багш, бүр цаашилбал нарсанд ч сууж явсан, овоо зайтай эр байсан гэдэг.

Тэрхүү Карданогийн зайгүй шалаанаас залхсан Тарталья эцэстээ гулдайж “хэнд ч хэлж болохгүй шүү” гэсэн ам өчиг авсны үндсэр дээр 3 зэргийн олон гишүүнтийн ерөнхий томъёогоо зааж өгчээ.

Тэгтэл төд удалгүй Кардано хээв нэг ам өчигөө эвдэн “Агуу илбэнүүд” гэсэн нэртэй ном хэвлэж, түүндээ мөнөөх томъёог нь оруулж орхих нь тэр.

Мэдээж хэрэг Тарталья дэлбэртлээ уурлаж, Карданог нүүр хийх газаргүй болтол нь шившиглэхээр шийдэн нээлттэй тэмцээнд зарлан дуудаж. Түүнд нь Кардано зальжин гэгч бултан зугатсаар, эцэстээ өөрийн шавь хэмээн Феррари (Ferrari) гэгч нэгэн залууг өмнөөсөө явуулав. Ингээд Тарталья Феррари хоёр нээлттэй тэмцээний талбарт халз үзэхээр болжээ. Гэвч Карданогийн явуулсан Феррари гэгч залуу бол үнэндээ 4 зэргийн олон гишүүнтийн ерөнхий томъёог ч олсон гоц авъяастан байсан ба, Тартальяг юм болголгүй дарж авах нь тэр. Ингэж Тартальягийн нэр алдар газарт унаж, Кардано Тартальягийн зуултаас ямар ч гарзгүй амжилттай мултарсан гэдэг.

Иймэрхүү түүхийн өрнөлүүдийн үр дүнд, өнөө үед 3 зэргийн олон гишүүнтийн ерөнхий томъёог “карданогийн томъёо” гэж нийтээр нэрлэж заншжээ (Харин 4 зэргийн олон гишүүнтийн ерөнхий томъёог Ферраригийн томъёог гэдэг).

Ингэхэд энэ хүртлэх яриаг сонсвол Кардано нь бусдын хийсэн юмыг булаан авсан нөхцөлгүй муу хүн гэж санагдаж болох юм. Гэвч нөгөөтэйгүүр математикийн судалгааны үр дүнг нуун хаацайлалгүй олонд таниулсан хүн гэгдэн үнэлэгдэх явдал ч бий.

Бодит байдал дээр, хэрвээ Тарталья аваар осолд ороод ч юм уу гэнэт үхээд өгсөн бол…, зовж олсон томъёо нь алдагдаж, хойчийн хүмүүс тэрийг нь хэрэг болгож дахин нээхгүй бол болохгүйд хүрнэ. Хэн нэг нь математикийн үр дүнг олонд зарлалгүй нууснаар хойчийн хүмүүст хэлж баршгүй гай болохыг ч байг гэх газаргүй шүү дээ.

Тиймийн учир Карданогийн явдлаас хойш, тэр мэт нууцлаг үзэлд бага багаар өөрчлөлт орж, алив томъёог нээсэн нэр хүндийг “түүнийг олсон хүнд бус, зарласан хүнд олгоно” гэсэн соёл тийш дэлгэрэн одсон байдаг.

Гэлээ гээд, хөлс хүчээрээ арай хийн олж нээсэн томъёог нь хөндлөнгийн хүн зөвшөөрөлгүй зарлаж, олны өмнө шившигт хутгуулаад дууссан Тартальягийн цээжний мухар ямар байхсан гэх билээ…